Bessere Auslosung für ganze Runden
Kürzlich habe ich mich ja mit den Möglichkeiten beim Auslosen auseinandergesetzt. Und festgestellt: So einfach, wie man denken möchte, ist es nicht. Z. B. kümmert sich tatsächlich – anders als im Release Announcement für Muckturnier 3.10.0 behauptet – das Programm eben nicht sowieso darum, dass man ganze Runden für Paare auslosen kann, und so lang es geht spielt keines mehrfach gegen ein anderes.
Wie funktioniert es bisher?
Die Auslosung passiert pro Anmeldung. Für eine ganze Runde wurden bis Version 3.8.0 einfach alle Plätze zufällig vergeben. Seither gibt es die Möglichkeit, die mehrfache Zulosung von Partnern (für Einzelspieler) und/oder Gegnern zu vermeiden.
Wie läuft das momentan ab? Beim Anklicken einer Anmeldung wird geschaut, welche Plätze verfügbar sind. Alle die, die „kollisionsfrei“ sind (also entsprechend der Einstellungen keinen bisherigen Partner und/oder Gegner enthalten) werden bevorzugt. Gibt es solche Plätze, dann wird einer von diesen gelost. Ansonsten ein komplett zufälliger. Seit Version 3.10.0 wird im Fall von Einzelspielern zweistufig ausgewählt: Wenn bisherige Parter und Gegner vermieden werden sollen, es aber keine solchen Plätze mehr gibt, dann wird zumindest nach Plätzen gesucht, bei denen bisherige Partner vermieden werden. Und erst dann wird zufällig ausgelost.
Bei der Auslosung einer ganzen Runde wird nichts anderes gemacht: Es wird eine zufällig sortierte Liste aller Anmeldungen generiert, und die dann von oben nach unten abgearbeitet – so, als ob man jede Anmeldung in einer zufälligen Reihenfolge anklicken würde.
Aber sorgt das tatsächlich für Kollisionsfreiheit? Nein. Einfaches Beispiel: Paar A kann nur noch gegen Paar B spielen, alle anderen Paarungen waren schon. beide stehen aber am Anfang der Liste, und werden an verschiedene Tische gelost (es gibt keine Kollision – die Tische sind ja noch leer). Und schon ist es vorbei – obwohl es noch eine Möglichkeit gegeben hätte.
Besserer Ansatz zum Auslosen ganzer Runden
Man muss die komplette Runde betrachten, nicht nur einzelne Plätze. Wer muss mit wem und gegen wen spielen, damit es keine Kollisionen gibt? Die einfachste Lösung hierfür ist der sog. „Brute Force“-Ansatz, das Ausprobieren aller Möglichkeiten. Das ist relativ einfach zu implementieren, mit einer Backtracking-Funktion, die sich rekursiv selbst aufruft, bis eine Lösung gefunden ist.
Funktionen, die sich selber immer wieder aufrufen, sind immer ein bisschen gefährlich, weil es zu sehr vielen Iterationen kommen kann. Also probieren wir es doch mal aus, und zählen die Aufrufe. Die Funktion selbst war wie gesagt recht leicht zu schreiben. Also Testlauf, aber gleich ordentlich – mit 50 Paaren.
Runde 1: Eh komplett zufällig ausgelost (da kann es ja noch keine Kollisionen geben). Runde 2: 26 Aufrufe. 3: 26. 4, 5, 6 … immer 26. Dann mal 786. Okay … und dann auf einmal über 800 000. Okay, zwar hat da selbst mein recht leistungsfähiger Desktop-Rechner kurz gestockt, aber das wäre schon noch okay. Aber: Wie viele Aufrufe können theoretisch maximal bei n Anmeldungen vorkommen?
Die Formel dafür ist einfach: (n - 1)!!. Für diesen Fall heißt das: Wir berechnen immer die Doppelfalkultät einer ungeraden Zahl, da ja immer eine gerade Anzahl an Anmeldungen angemeldet sein muss (egal ob feste Paare oder Einzelspieler). Also multipliziert man alle ungeraden Zahlen bis n - 1 miteinander, für n = 6 wäre das z. B. 1 · 3 · 5.
Sieht doch übersichtlich aus, oder? Was wäre das für 10? 9!!, das sind 945. Geschenkt. Und für 20? 19!!, das sind 654 729 075. Oha, da kommen wir schon in den mittleren Millionenbereich. Und für 50?! Soll ja durchaus mal ein Turnier mit 50 Paaren geben? Tatsächlich sind 49!! sage und schreibe 58 435 841 445 947 272 053 455 474 390 625 – eine Zahl mit 32 Stellen. Den Namen musste ich mir erstmal überlegen – wenn ich mich nicht verzählt habe, dann sprechen wir hier von gut 58 Quintillionen Funktionsaufrufen im schlechtesten Fall bei 50 Anmeldungen. Das ist selbstverständlich so nicht mehr darstellbar.
Eine funktionierende Implementierung
Glücklicherweise haben sich schon lang vor mir viel schlauere Leute als ich mit solchen Problemen auseinandergesetzt. Das, was wir hier machen wollen, ist – mathematisch betrachtet – die Berechnung der maximalen Paarung in einem ungerichteten Graphen, wobei jedes Paar bzw. jeder Spieler einen Knoten darstellt, der mit jedem möglichen anderen Paar- bzw- Spieler-Knoten durch eine Kante verbunden ist.
Beispiel: Wir haben sechs Paare, „A“ bis „F“. In der ersten Runde hat A gegen B gespielt, C gegen D und E gegen F. Dann würde die Visualisierung eines Graphen, der alle noch möglichen Paarungen beinhaltet, folgendermaßen aussehen:
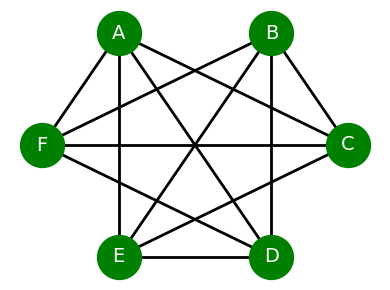
Nur wie berechnet man nun die maximale Paarung? Ohne dass im schlechtesten Fall eine irrwitzige Rechenleistung dafür nötig wäre? Die Lösung ist Edmonds’ Blossom Algorithm. Der tut exakt das: Die maximale Paarung in einem ungerichteten Graphen berechnen. Eine schöne Erklärung für das, was dabei passiert – incl. Visualisierung – gibt es bei der TU München. Ich persönlich finde das sehr beeindruckend, wie man auf sowas kommt – vor allem, wenn man bedenkt, dass der Algorithmus bereits 1965 veröffentlicht wurde!
Für das obige Beispiel wäre, wenn man die Paare in alphabetischer Reihenfolge abarbeitet, die durch den Algorithmus berechnete, maximale Paarung folgende (die gepaarten Kanten sind rot hervorgehoben):
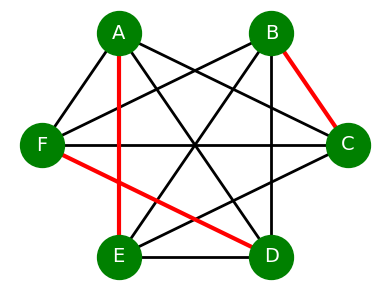
In der nächsten Runde würden diese Kanten dann fehlen (die Paarung gab es ja dann bereits), und die berechnete maximale Paarung würde so aussehen:
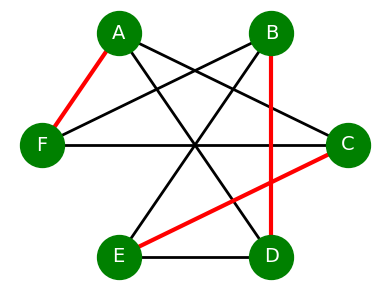
Um für hinreichende Zufälligkeit zu sorgen, kann man die Knoten vorher zufällig sortieren, so dass der Algorithmus nicht immer beim selben Paar oder Spieler mit der Suche beginnt, und das Ergebnis nicht bereits allein aus der gegebenen Konstellation vorhersagbar ist.
Aber Sorgt das dafür, dass wirklich alle Möglichkeiten ausgenutzt werden können, die es rein rechnerisch gibt? Leider nein. der Algorithmus betrachtet nur die aktuelle Situation. Nicht das, was vorher war, und auch nicht das, was hinterher noch kommen könnte. Das kann bei ungünstigen Konstellationen dazu führen, dass man sich eine Möglichkeit „verbaut“ und es so schon zu Kollisionen kommen kann, bevor die theoretisch möglichen Runden erreicht werden. Würde man wirklich alle Möglichkeiten ausnutzen wollen, müsste man im Vorfeld das komplette Turnier in einem Round-Robin-Design planen. Das hat dann allerdings nichts mehr mit einer Auslosung zu tun.
Aber es geht ja auch gar nicht um das theoretisch maximal Machbare. So viele Runden wollen wir ja zumeist gar nicht spielen. Sicher ist: Dieser Ansatz bringt eine erhebliche Verbesserung für die Auslosung ganzer Runden, und erheblich weniger Kollisionen, als das, was wir bisher hatten. Alle Anmeldungen werden zunächst zufällig sortiert; somit ist die Zuordnung – im Rahmen dessen, was mit einer maximalen Paarung möglich ist – auch wirklich noch zufällig.
Wie funktioniert es also jetzt?
Die 1. Runde wird, egal ob man mit festen Paaren oder Einzelspielern spielt, immer komplett zufällig ausgelost. Hier kann es ja noch keine Kollisionen geben.
Bei festen Paaren ist die einzige Möglichkeit, Kollisionen zu vermeiden, dass ein Paar nicht mehrfach gegen ein anderes spielt. Die Paare werden zufällig sortiert, und dann wird eine maximale Paarung ermittelt. Bleiben Paare übrig, werden diese komplett zufällig einander zugelost.
Bei Einzelspielern kann man entweder gleiche Partner oder gleiche Gegner vermeiden – oder beides.
Zunächst werden die Spieler zu Paaren zugeordnet. Je nach Einstellung entweder komplett zufällig, oder analog wie oben bei festen Paaren beschrieben – nur, dass hier nicht auf die bisherigen Gegner, sondern auf die bisherigen Partner geschaut wird.
Im zweiten Schritt werden dann die ausgelosten Paare einander zugeordnet. Wie das passiert, hängt wieder von den Einstellungen ab: Entweder es werden die Paare komplett zufällig zugelost, oder es wird nach einer maximalen Paarung gesucht, wobei kein Spieler auf einen Gegner treffen soll, gegen den er schon einmal gespielt hat. Gibt es hier keine vollständige Lösung mehr (und das geht, abhängig von der Zahl der Spieler, recht schnell), wird jeweils eine Möglichkeit gesucht, bei der zumindest Spieler 1 bzw. Spieler 2 keine Gegner mehrfach sieht (ob ein Spieler 1 oder 2 wird, ist ja im 1. Schritt zufällig zugeordet worden). Das deckt zwar bei Weitem nicht alle möglichen Kombinationen ab – aber das Problem ist tatsächlich so komplex, dass man es nur schwer beherrschen kann. Die Vorgabe zumindest zur Hälfte zu erfüllen scheint mir da ein guter Kompromiss zu sein. Es wird immer die Variante mit den wenigsten Kollisionen gewählt.
Und ab wann gibt es das?
Die neue Funktionalität wird, ganz heimlich, still und leise, im nächsten Release verfügbar sein. Das wird vermutlich 3.11.0 heißen (t. b. a.). Für den Benutzer ändert sich augenscheinlich nichts, alles passiert „unter der Haube“. Außer, dass es jetzt eben bei der Auslosung ganzer Runden erheblich weniger Kollisionen geben sollte, wenn man die entsprechenden Optionen aktiviert hat.