Möglichkeiten beim Auslosen

23.05.2025

Seit Version 3.8.0 gibt es die Möglichkeit, nicht nur einfach zufällig auszulosen, sondern die Auslosung mit Regeln zu versehen – sofern für jede Runde ausgelost wird. Namentlich kann man angeben, dass nach Möglichkeit die Zulosung von Gegnern vermieden wird, gegen die schon einmal gespielt wurde, und für Einzelspieler auch die von Partnern, die der Spieler schon einmal hatte.

Es stellt sich die Frage, wie viele Möglichkeiten es überhaupt gibt – also wie viele Runden gespielt werden können, bevor es zu einer „Kollision“ kommt. Jetzt sollte man aus dem Mucken keine Wissenschaft machen, aber hier braucht es ein bisschen Mathematik, namentlich Kombinatorik ;-)

Nennen wir die Anzahl der Anmeldungen (Paare oder Spieler) n und die maximale Anzahl Runden ohne Kollisionen r. Diese unterscheidet sich je nach Turniermodus und Einstellungen:

Feste Paare

Für feste Paare ist es relativ einfach. Eine Kollision bei Partnern kann es nicht geben, da ja eh immer dieselben Spieler zusammenspielen. Also muss man sich nur die Gegner anschauen – in diesem Fall die gegnerischen Paare.

Neben der Auslosungsvariante „Paar 1 bleibt sitzen, Paar 2 rutscht weiter“ ist eine zufällige Auslosung mit der Einschränkung, dass dieselben Gegner vermieden werden sollen, interessant.

Prinzipiell muss eine gerade Anzahl Paare angemeldet sein. Es gilt also:

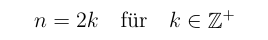
$n = 2k \text{\hspace{1em}für\hspace{1em}} k \in \mathbb{Z}^+$

Paar 1 bleibt sitzen, Paar 2 rutscht weiter

Hierfür brauchen wir keine höhere Mathematik. Es gibt halb so viele Tische wie Paare, da immer zwei Paare an einem Tisch sitzen. Alle Paare 2 rutschen jede Runde einen Tisch weiter. Also können halb so viele Runden gespielt werden, wie es Paare gibt, bevor das Paar 2 von Tisch 1 wieder an Tisch 1 sitzt und sich somit die Gegner wiederholen würden. Also gilt hier:

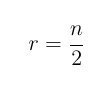
$r = \frac{n}{2}$

Beispiel für Für 6 Paare (a, b, c, d, e, f):

Runde	Tisch	Paare
1	1	a – b
	2	c – d
	2	e – f
2	1	a – f
	2	c – b
	3	e – d
3	1	a – d
	2	c – f
	3	e – b

In Runde 4 würde Paar b wieder zu Tisch 1 weiterrücken und erneut gegen Paar a spielen. Die maximale Rundenanzahl kann definitv erreicht werden, da sie von vornherein feststeht und nicht mehr durch eine Auslosung beeinflusst wird.

Gleiche Gegner vermeiden

Wird zufällig ausgelost, und es soll vermieden werden, dass dieselben Paare mehrfach gegeneinander spielen, dann muss die maximale Anzahl an möglichen Paarungen betrachtet werden. Diese sind:

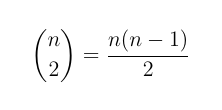
$\binom{n}{2} = \frac{n(n-1)}{2}$

Da in jeder Runde an halb so vielen Tischen gespielt wird, wie es Paare gibt, errechnet sich die maximale Anzahl der kollisonsfreien Runden dann zu:

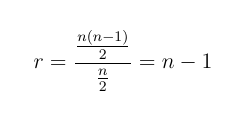
$r = \frac{\frac{n(n-1)}{2}}{\frac{n}{2}} = n-1$

Es kann also theoretisch kollisionsfrei eine Runde weniger gespielt werden, als Paare angemeldet sind. Allerdings kann es passieren, dass, bedingt durch eine ungünstige Konstellation, eine Paarung in einer früheren Runde eine spätere Paarung verhindert. Es kann also passieren, dass nicht alle Möglichkeiten tatsächlich auch ausgenutzt werden können.

Hier ein Beispiel für Für 4 Paare (a, b, c, d):

Runde	Tisch	Paare
1	1	a – b
1	2	c – d
2	1	a – c
2	2	b – d
3	1	a – d
3	2	b – c

Einzelspieler

Für einzelne Spieler wird es etwas komplizierter. Wie gesagt haben wir hier die Möglichkeit, sowohl Wiederholungen bei Partnern, bei Gegnern sowie die Kombination aus beidem zu vermeiden.

Grundsätzlich muss eine durch 4 teilbare Anzahl an Spielern angemeldet sein, somit gilt:

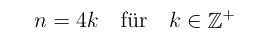
$n = 4k \text{\hspace{1em}für\hspace{1em}} k \in \mathbb{Z}^+$

Keine gleichen Partner

Sollen nur gleiche Partner vermieden werden, die Gegner sind aber egal, dann haben wir dieselbe Situation wie bei den festen Paaren – nur dass wir eben nicht Paare betrachten, die gegeneinander, sondern Spieler, die miteinander spielen.

Die maximale Anzahl an kollisionsfreien Paaren für n Spieler ist:

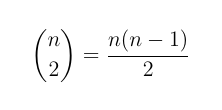
$\binom{n}{2} = \frac{n(n-1)}{2}$

Da in jeder Runde jeder Spieler mit genau einem anderen Spieler spielt, gibt es pro Runde halb so viele Paare, wie es Spieler gibt. Somit errechnet sich die theoretische maximale Anzahl kollisionsfreier Runden (analog zu der Situation bei den festen Paaren) zu:

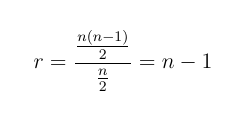
$r = \frac{\frac{n(n-1)}{2}}{\frac{n}{2}} = n-1$

Auch hier gilt, dass die maximale Rundenanzahl je nach Verlauf der Auslosung womöglich nicht erreicht werden kann. Beispiel innerhalb einer Runde: Wenn für Spieler a nur noch Spieler b als noch nicht „verbrauchter“ Partner übrig ist, beide aber am Anfang der Auslosung in verschiedene Paare oder an verschiedene Tische gelost werden, können Kollisionen nicht mehr vermieden werden.

Hier ein Beispiel für 8 Spieler (a, b, c, d, e, f, g, h):

Runde	Tisch	Paare
1	1	a / b – c / d
1	2	e / f – g / h
2	1	a / c – b / d
2	2	e / g – f / h
3	1	a / d – b / c
3	2	e / h – f / g
4	1	a / e – b / f
4	2	c / g – d / h
5	1	a / f – b / e
5	2	c / h – d / g
6	1	a / g – b / h
6	2	c / e – d / f
7	1	a / h – b / g
7	2	c / f – d / e

Keine gleichen Gegner

Sollen nur gleiche Gegner vermieden werden, gleiche Partner sind aber egal, muss beachtet werden, dass ein Spieler pro Runde auf zwei Gegner trifft. Es gibt außer dem Spieler, um den es geht, noch n - 1 andere Spieler. Da es ja aber immer zwei sind, berechnet sich die theoretische maximale Anzahl Runden, bevor sich ein Gegner wiederholt zu:

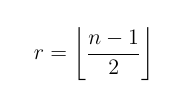
$r = \left\lfloor { \frac{n-1}{2} } \right\rfloor$

Hier ein Beispiel für 8 Spieler. Es wiederholen sich zwar Paare, die zusammenspielen, aber jeder Spieler spielt für sich nur ein einziges Mal gegen einen anderen:

Runde	Tisch	Paare
1	1	a / b – c / d
1	2	e / f – g / h
2	1	a / h – b / g
2	2	e / f – c / d
3	1	c / d – g / h
3	2	e / f – a / b

Wieder haben wir hier nur ein theoretische Maximum. Ob diese Rundenzahl tatsächlich kollisionsfrei erreicht werden kann, hängt davon ab, wie die Partner zugelost werden – und darauf wird ja nicht geachtet.

Weder gleiche Partner, noch gleiche Gegner

Hier wird es schwierig. Als Ansatz könnte man sagen, dass auf jeden Fall so viele Runden möglich sein müssten, wie ein Spieler immer auf drei neue Mitspieler treffen kann – egal in welcher Konstellation. Damit wäre definitiv ausgeschlossen, dass sich Partner oder Gegner wiederholen – es sind ja immer drei Spieler, auf die der jeweilige Spieler noch nicht getroffen ist.

Nach einiger Recherche habe ich herausgefunden, dass es sich bei dieser Überlegung exakt um das Social-Golfer-Problem handelt, in diesem Fall für Vierergruppen. Allein das ist schon eine kombinatorisch so komplexe Fragestellung, dass man die Lösung nicht mehr berechnen, sondern nur annähern kann.

Ein bekannter Ansatz für dieses Problem ist, dass die theoretische maximale Anzahl an Runden (was den Wochen beim Social-Golfer-Problem entspricht) folgendermaßen abgeschätzt werden kann:

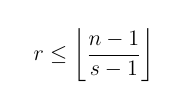
$r \leq \left\lfloor { \frac{n-1}{s-1} } \right\rfloor$

Wobei s die Gruppengröße ist, in unserem Fall also 4. Das ist allerdings tatsächlich nur eine Näherung. Wenn man z. B. die theoretisch zwei möglichen Runden für 8 Spieler konstruieren will, wird man feststellen, dass das tatsächlich für diesen Fall nicht möglich ist.

Für „weder gleiche Partner, noch gleiche Gegner“ dürfte es mehr Möglichkeiten als das geben, da nicht ausgeschlossen ist, dass ein oder mehrere Spieler mehrfach miteinander am Tisch sitzen. Es kommt ja auf die ausgelosten Beziehungen der Spieler an, ob es trotzdem keine Kollision gibt. Allerdings ist ja schon das vermeintlich einfache Social-Golfer-Problem schon nicht zu beherrschen. Zusätzliche Regeln erhöhen die Komplexität hier noch weiter. Allenfalls ist hier vielleicht eine Annäherung der Maximalanzahl der Runden möglich – wenn überhaupt.

Konstruiert man die Zusammenstellung der Paare und ihrer Gegner sorgfältig, sind ungeachtet dessen z. B. für 8 Spieler folgende 3 Runden möglich, in denen weder ein Spieler mehrfach mit, noch gegen einen anderen spielt:

Runde	Tisch	Paare
1	1	a / b – c / d
1	2	e / f – g / h
2	1	a / e – b / f
2	2	c / g – d / h
3	1	a / d – e / h
3	2	b / c – f / g

So eine Auslosung per Zufall zu erhalten halte ich für annähernd ausgeschlossen. Sie programmatisch zu generieren wäre vermutlich möglich, wenngleich bei einem „Brute-Force“-Ansatz, also dem einfachen Ausprobieren aller möglichen Kombinationen, die Anzahl der nötigen Rechenoperationen mit steigender Spieleranzahl vermutlich sehr schnell ins Unendliche abdriftet.

Fazit

Bei festen Paaren ist die Lage relativ übersichtlich. Wenn mit einem festen Schema („Paar 1 bleibt sitzen, Paar 2 rutscht weiter“) gespielt wird, dann gibt es nur eine Auslosung in der 1. Runde. Die maximale Anzahl Runden ist berechenbar und kann definitiv auch erreicht werden. Dasselbe gilt für das zufällige Auslosen, wenn gleiche Gegner vermieden werden sollen: Wir können die theoretische maximale Rundenzahl berechnen; allerdings kann es schon hier – abhängig vom Verlauf der Auslosung – passieren, dass man diese nicht erreicht.

Bei einzelnen Spielern wird es komplexer. Sofern nur gleiche Partner oder gleiche Gegner vermieden werden sollen, ist die maximale Anzahl der Runden zwar berechenbar, aber ob sie tatsächlich erreicht wird, hängt wieder davon ab, wie die Auslosung verläuft. Schwierig wird es, wenn gleiche Partner und gleiche Gegner vermieden werden sollen: Hier wird die Problemstellung so komplex, dass eine einfache Berechnung der maximalen Rundenzahl nicht mehr möglich ist.

Trotz der vermeintlich einfachen Fragestellung handelt es sich hier teilweise tatsächlich um hochkomplexe kombinatorische Probleme, für die es zum Teil schlicht keine Lösung gibt.

News